1.Multiplication and Division tricks; GENERAL APTITUDE
1.Multipication tricks-
Multiplication by 5
Multiply the number by 10/2 because 5 = 10/2.
Examples:
- 46×5 = 460/2 = 230
- 106×5 = 1060/2 = 53
- 27×5 = 270/2 = 135
Multiplication by 25
Multiply the number by 100/4 because 25 = 100/4.
Examples:
- 36×25 = 36×100/4 = 900
- 64×25 = 64×100/4 = 1600
- 17×25 = 17×100/4 = 425
Multiplication by 125
Multiply the number by 1000/8 because 125 = 1000/8.
Example:
- 72×125=72×1000/8=9000
- 112×125=112×1000/8=14000
- 42×125=42×1000/8=5250
Multiplication of two digit number having same unit digit
Let’s understand with the help of an example.
Let’s calculate answer of 63 X 43
- Step 1: In the first step multiply unit place digit of both the number it is our last two digits.
- Step 2: In the second step multiply 6×4=24, now add 3 in 24 (24+3 = 27), so 27 will be our first two digits.
Therefore answer is 2709.
Example:
- 35×75 = 2625
- 21×31 = 701
Multiplication with the number having 5 at units place
Let’s understand with the help of an example.
Let’s calculate answer of 34 X 15
34×15 = 34/2×30 = 510
Explanation: Divide the first number by 2 and double the number having unit place 5.
Example:
- 26×45 = 26/2×90 = 13×90 = 1170
- 27×35 = 26/2×70 = 910+35 = 945
- 17×25 = 16/2×50 = 8×50= 400+25 = 425
Multiplication number under twenty
Let’s take example to calculate the answer of 12×14
- Step 1: Multiply the numbers at unit place i.e. 2×4 = 08.
- Step 2: Now add the first number and unit digit of second number i.e. 12+4 = 16
- Step 3: Now combine step 2 and 1 so that answer is 16&08. 16 will be first two digits of the answer and 8 will be the last digit.so 168
Example:
- 13×12 = 156
-MULTIPLY ANY 2 DIGIT NUMBERS-
Step 1 : Multiply the digits in the unit place, that is 2×1=2. This will be the unit digit of the answer as well.
Step 2 : Now this is important. Now, we cross-multiply the numbers 3×1=2 and 2×2=4 and add them. This is why it is referred to as the term criss-cross multiplication. Write 7 in the 10’s place of the answer.
Step 3 : This is the last step. You just multiply the digits in the 10’s place, that is 3×2=6.
So, the product will be :
The complete steps involved in the calculation can be illustrated in the following figure.
If you practice this shortcut, you can multiply the any 2 -digit numbers mentally without actually doing any computation.
Let’s take another example. Let’s consider the multiplication 47×32. The complete steps involved in the calculation is illustrated in the figure:
Notice the carry-forward in each step. It is important to note that only 1 digit should be retained in each steps. The rest is carry forward.
Important Note :
Number of steps involved in the criss-cross multiplication = 2x(number of digits) – 1
- For 2-digit multiplication, number of steps : 2×2- 1 = 3
- For 3-digit multiplication, number of steps : 2×3- 1 = 5
- For 4-digit multiplication, number of steps : 2×4- 1 = 7
So, the product will be :
-MULTIPLY ANY 3 DIGIT NUMBERS-
The number of steps in a 3 x 3 multiplication is 5. Let’s understand the steps with an example.
Example : Suppose you want to multiply 132 x 214.
Step 1 : Write the numbers one below the other. Multiply the digits in the unit place as in 2×2 multiplication, that is 2×4=2. This will be the unit digit of the answer as well.
Step 2 : Now, cross multiply the digits in the 10’s and unit’s place to get the digit in the 10’s place of the answer.
Step 3 : Now, notice the criss-cross multiplication. Here, we multiply the terms (1×4), (2×2) and (3×1) and then add these terms to get 11.
Step 4 : Now, repeat Step 2 with the digits in the 100’s and the 10’s place.
Step 5 : This is the last step in the multiplication. Now, repeat Step 1 with the digits in 100’s place.
The complete steps involved in the calculation is illustrated in the figure :
Notice the carry-forward in each step.
On the similar lines, can you multiply,
- 423 x 234
- 124 x 465
- 567 x 890
- 646 x 772
Step 2 : Now, cross multiply the digits in the 10’s and unit’s place to get the digit in the 10’s place of the answer.
Step 3 : Now, notice the criss-cross multiplication. Here, we multiply the terms (1×4), (2×2) and (3×1) and then add these terms to get 11.
Step 4 : Now, repeat Step 2 with the digits in the 100’s and the 10’s place.
Step 5 : This is the last step in the multiplication. Now, repeat Step 1 with the digits in 100’s place.
The complete steps involved in the calculation is illustrated in the figure :
-MULTIPLY ANY 4 DIGIT NUMBERS-
Now Let’s try to understand the criss-cross multiplication technique to multiply any 4 digit numbers. As you know, the number of steps when multiplying any 4-digit numbers is 7.
Let us consider a simple example 3215 x 4231.
The step-by-step procedure can be explained with the following figure:
Notice the carry-forward in each stage of the multiplication. I hope, The steps are self – explanatory. Notice the additional steps compared to 2 x 2 and 3 x 3 multiplication.
Exercise : On the similar lines, can you multiply?
- 2318×1339
- 7222×4223
- 9222×9229
- 5216×1265
Now Let’s try to understand the criss-cross multiplication technique to multiply any 4 digit numbers. As you know, the number of steps when multiplying any 4-digit numbers is 7.
Let us consider a simple example 3215 x 4231.
The step-by-step procedure can be explained with the following figure:
Notice the carry-forward in each stage of the multiplication. I hope, The steps are self – explanatory. Notice the additional steps compared to 2 x 2 and 3 x 3 multiplication.
Exercise : On the similar lines, can you multiply?
- 2318×1339
- 7222×4223
- 9222×9229
- 5216×1265
Multiplication when the number of digits are unequal
If the number of digits in multiplicand and multiplicand is unequal, you add zeros so that the digits have the same number of digits.
Let us consider an example. Suppose you have to multiply 4125 x 511. So, the number of digits are 4 and 3 respectively.
So, we convert 511 to 05111 and use this technique.
Exercise : Can you multiply?
- 12 x 145
- 222 x 4223
- 92 x 9
- 52 x 125
Multiplication with 9, 99,999 etc..
Examples:
- 13*9=13*(10-1)=130-13=117
- 26*99=26*(100-1)=2600-26=2574
- 350*999=350*(1000-1)=350000-350=349650
- 13*9=13*(10-1)=130-13=117
- 26*99=26*(100-1)=2600-26=2574
- 350*999=350*(1000-1)=350000-350=349650
2.Division tricks-
Divisibility Test
Divisibility Test for 2
A number is divisible by 2 if the last digit is divisible by 2 i.e. last digit is 0, 2, 4, 6 or 8.
E.g. 864 is divisible by 2 since the last digit 4 is divisible by 2.
E.g. 864 is divisible by 2 since the last digit 4 is divisible by 2.
Divisibility Test for 3
A number is divisible by 3 if the sum of the digits of the number is divisible by 3.
E.g. 861 is divisible by 3 since the sum of the digits is 15 (8 + 6 + 1 = 15), and 15 is divisible by 3.
E.g. 861 is divisible by 3 since the sum of the digits is 15 (8 + 6 + 1 = 15), and 15 is divisible by 3.
Divisibility Test for 4
A number is divisible by 4 if the number formed by the last two digits is divisible by 4.
E.g. 504 is divisible by 4 since 04 is divisible by 4.
E.g. 504 is divisible by 4 since 04 is divisible by 4.
Divisibility Test for 5
A number is divisible by 5 if the last digit is either 0 or 5.
E.g. 425 is divisible by 5 since the last digit is 5.
E.g. 425 is divisible by 5 since the last digit is 5.
Divisibility Test for 6
A number is divisible by 6 if it is divisible by 2 AND it is divisible by 3.
E.g. 186 is divisible by 6 since it is divisible by 2 AND it is divisible by 3.
E.g. 186 is divisible by 6 since it is divisible by 2 AND it is divisible by 3.
Divisibility Test for 7
To find out if a number is divisible by 7 or not, follow these steps:
1. Separate the last digit from the rest of the number. Let us call the rest of the number the truncated number. The truncated number has one less digit than the original number or the previous truncated number.
2. Double the last digit and subtract it from the truncated number.
3. Check if this result is sufficiently small so that you can immediately say if this is divisible by 7. If it is divisible by 7, then so was the original number. If it is not divisible by 7, then neither was the original number.
4. If the number is still too large to visually check if it is divisible, apply this rule over and over again as necessary.
1. Separate the last digit from the rest of the number. Let us call the rest of the number the truncated number. The truncated number has one less digit than the original number or the previous truncated number.
2. Double the last digit and subtract it from the truncated number.
3. Check if this result is sufficiently small so that you can immediately say if this is divisible by 7. If it is divisible by 7, then so was the original number. If it is not divisible by 7, then neither was the original number.
4. If the number is still too large to visually check if it is divisible, apply this rule over and over again as necessary.
E.g. Check 6132. The last digit is 2 and the truncated number is 613. Twice of 2 is 4. So subtract 4 from the truncated number 613 i.e. 613 – 4 = 609. Again, the last digit is now 9, and the truncated number is 60. Twice of 9 is 18. Subtract it from the truncated number 60, i.e. 60 – 18 = 42. Now 42 is small enough to check visually. We know that 42 is divisible by 7, so we can tell that 6132 is divisible by 7 also.
NOTE: Explaining this step is long. But actually using it is a very short and time saving method. This method is especially useful in Geometry and Mensuration problems where the value of π plays an important role.
Divisibility Test for 8
A number is divisible by 8 if the number formed by the last three digits is divisible by 8.
E.g. 8120 is divisible by 8 since 120 is divisible by 8.
E.g. 8120 is divisible by 8 since 120 is divisible by 8.
Divisibility Test for 9
A number is divisible by 9 if the sum of its digits is divisible by 9. If the sum is large, you can once again add the digits and check if the new sum is divisible by 9.
E.g. 27549 is divisible by 9 since the sum of the digits is 27 (2 + 7 + 5 + 4 + 9 = 27), and 27 is divisible by 9.
E.g. 27549 is divisible by 9 since the sum of the digits is 27 (2 + 7 + 5 + 4 + 9 = 27), and 27 is divisible by 9.
Divisibility Test for 10
A number is divisible by 10 if the last digit is 0.
E.g. 1760 is divisible by 10 since the last digit is 0.
E.g. 1760 is divisible by 10 since the last digit is 0.
Divisibility Test for 11
Method 1:- The (sum of the odd place digits) – (sum of the even place digits) is divisible by 11.
E.g. 963391
Sum of odd place digits = 9 + 3 + 9 = 21
Sum of even place digits = 6 + 3 + 1 = 10
Difference = 21 – 10 = 11 which is divisible by 11.
So, yes, 963391 is divisible by 11.
Sum of odd place digits = 9 + 3 + 9 = 21
Sum of even place digits = 6 + 3 + 1 = 10
Difference = 21 – 10 = 11 which is divisible by 11.
So, yes, 963391 is divisible by 11.
Method 2: Subtract the last digit from the remaining truncated number. If the result is divisible by 11, then so was the first number. Apply this rule over and over again as necessary.
E.g. 963391 → 96339 – 1 = 96338 → 9633 – 8 = 9625 → 962 – 5 = 957 → 95 – 7 = 88, which is divisible by 11. So yes, 963391 is divisible by 11.
E.g. 963391 → 96339 – 1 = 96338 → 9633 – 8 = 9625 → 962 – 5 = 957 → 95 – 7 = 88, which is divisible by 11. So yes, 963391 is divisible by 11.
Divisibility Test for 13
To find out if a number is divisible by 13 or not, follow these steps:
- Separate the last digit from the rest of the number. Let us call the rest of the number the truncated number. The truncated number has one less digit than the original number or the previous truncated number.
- Multiply the last digit by 4 and add it to the truncated number.
- Check if this result is sufficiently small so that you can immediately say if this is divisible by 13. If it is divisible by 13, then so was the original number. If it is not divisible by 13, then neither was the original number.
- If the number is still too large to visually check if it is divisible, apply this rule over and over again as necessary.
E.g. 12675 → 1267 + 20 = 1287 → 128 + 28 = 156 → 15 + 24 = 39, which is divisible by 13. So yes, 12675 is divisible by 13.
Divisibility Test for 17
To find out if a number is divisible by 17 or not, follow these steps:
- Separate the last digit from the rest of the number. Let us call the rest of the number the truncated number. The truncated number has one less digit than the original number or the previous truncated number.
- Multiply the last digit by 5 and subtract it from the truncated number.
- Check if this result is sufficiently small so that you can immediately say if this is divisible by 17. If it is divisible by 17, then so was the original number. If it is not divisible by 17, then neither was the original number.
- If the number is still too large to visually check if it is divisible, apply this rule over and over again as necessary.
E.g. 21165 → 2116 – 25 = 2091 → 209 – 5 = 204 → 20 – 20 = 0, which is divisible by 17. So yes, 21165 is divisible by 17.
Divisibility Test for 19
Add two times the last digit to the remaining leading truncated number. If the result is divisible by 19, then so was the first number. Apply this rule over and over again as necessary.
E.g. 185117 → 18511 + 2 × 7 = 18525 → 1852 + 2 × 5 = 1862 → 186 + 2 × 2 = 190, which is divisible by 19. So yes, 185117 is divisible by 19.
Divisibility Test for Composites
A number is divisible by a composite if it is also divisible by all the prime factors.
E.g. 157905 is divisible by 33 if it is divisible by 3 AND by 11.
Tricks-
LONG DIVISION METHOD-
In the fast long division method, we will be dealing a lot with two digit numbers. The left hand digit of the number is the tens digit and the right hand digit is the units digit. We will refer to the tens digit with "T" and the units digit as "U" and we will refer to the whole two digit number as "N" for the number.
We will also be dealing with pairs of two digit numbers and to create the NT (Number - Tens) product we take the whole number (N) of one two digit number and add it to the tens (T) digit of the other two digit number.
The N number comes from multiplying the tens digit of the divisor by the first digit of the answer. The T number comes from multiplying the units digit of the divisor by the first digit of the answer. The N and T numbers are then added together to give us our NT value.
We will also refer to a "partial dividend" which is a number will lead us to the next digit of the answer by dividing it by the first digit of the divisor. The partial dividend will also lead us to the tens digit of the next working figure.
The "working figure" is a number whose purpose is to find the next partial dividend.
In explaining the fast division method, we will be writing everything down and to show where numbers are copied we include arrows. In practice when doing this method, not everything needs to be written down. At first, you may find it necessary to write down everything, but as you become accustomed to the method, you will find it easy to start to omit writing down some of the working figures. Your goal should be to become proficient enough with the fast division method that you do not need to write anything down except the answer.
Here is a video on Fast Division using two digit divisors.
Division With Two Digit Divisors
Let's use 4712 divided by 31 as our example as we explain the method.
Step 1
Divide the first figure of the dividend by the first figure of the divisor and the result is the first figure of the answer.
There are some points to remember for this step:
- If the first figure of the dividend is smaller than the first figure of the divisor then use the first two figures of the dividend.
- If the second digit of the divisor is 8 or 9 then add 1 to the value of the first figure of the divisor and divide the dividend by this new figure.
- Always ignore any remainder as we are only interested in the whole number value from the division.
The first figure of the dividend is 4, and the first figure of the divisor is 3. Dividing 4 by 3 we get 1 as the first figure of our answer.
The 4 is also our first partial dividend, so we will copy it down to what will be our partial dividend row below the dividend
The 4 is also our first partial dividend, so we will copy it down to what will be our partial dividend row below the dividend
Step 2
Calculate the NT product by multiplying the divisor by the first figure we have for the answer.
We subtract this NT product from the first partial dividend from step 1.
We will write the 1 just below and to the left of the next figure in the dividend, the 7. This 1 will be the tens digit of our first working figure.
Step 3
We bring down the next figure of the divisor, the 7, down next to the 1 to create our first working figure, 17.
We now calculate the U product by multiplying the units figure of the divisor by the first figure we have for the answer.
We subtract the U product from the working figure to get the second partial dividend.
So 16 is our next partial dividend, and we will write it below the 17 on our partial dividend row.
Step 4
We now divide the second partial dividend, the 16, by the first figure of the divisor to get the second figure of our answer.
The following steps are just repeating steps 2, 3 and 4 using the latest found figure of the answer.
Step 5
Calculate the NT product by multiplying the divisor by the second figure we have for the answer.
We subtract this NT product from the second partial dividend from step 3.
We will write the 1 just below and to the left of the next figure in the dividend. This 1 will be the tens digit of our second working figure.
Step 6
We bring down the next figure of the divisor, the 1, down next to the 1 to create our second working figure, 11.
We now calculate the U product by multiplying the units figure of the divisor by the second figure we have for the answer.
We subtract the U product from the working figure to get the third partial dividend.
So 6 is our next partial dividend, and we will write it below the 11 on our partial dividend row.
Step 7
We now divide the third partial dividend, the 6, by the first figure of the divisor to get the third figure of our answer.
We have the answer at this point the remaining steps are to see if there is any remainder.
Remainder Step 1
Calculate the NT product by multiplying the divisor by the third figure we have for the answer.
We subtract this NT product from the third partial dividend from step 6.
We will write the 0 just below and to the left of the last figure in the dividend. This 0 will be the tens digit of our third working figure.
Remainder Step 2
We bring down the next figure of the divisor, the 2, down next to the 0 to create our third working figure, 02.
We now calculate the U product by multiplying the units figure of the divisor by the third figure we have for the answer.
We subtract the U product from the working figure to get the fourth partial dividend.
Our fourth partial divisor is zero which means we have no remainder in this example.
The answer to 4712 divided by 31 is 152 with no remainder.
The answer to 4712 divided by 31 is 152 with no remainder.
Division Correction - Answer Too Small
The partial dividend can inform us that the latest figure of the answer is too small. If the partial dividend is equal to or greater than the divisor, then the latest figure of the answer is too small.
This time, we will look at 18096 divided by 29.
Step 1
We need to divide the first figure of the dividend by the first figure of the divisor.
Firstly, the first figure of the dividend is 1 while the first figure of the divisor is 2 and we cannot divide 1 by 2 so we must use the first two figures of the dividend which is 18.
Secondly, we are dividing by 29, so the second figure of the divisor is 9 so instead of dividing by 2 we instead divide by 3.
So 6 is the first figure of the answer.
We used 18 divided by 3 above, we will copy 18 down as our first partial dividend.
Step 2
We now calculate the NT product by multiplying the divisor by the first figure we have for the answer, which is 6.
Multiplying 2 by 6 we get the N value of 12 and multiplying 9 by 6 we get the T value of 5, adding these together we get the NT value of 17.
We subtract the NT value from our partial dividend, 18 - 17 = 1, so we put the 1 up in the working figure row below the next figure in the dividend, the zero.
Step 3
We bring down the next figure in the dividend, the zero, and we have our first working figure of 10.
We now calculate the U product by multiplying the units figure of the divisor, the 9, by the first figure we have for the answer, the 6.
The U-value is the unit figure of the result of the multiplication, in this case, 4. We subtract the U value from the working figure.
The 6 is our second partial dividend.
Step 4
We now divide the second partial dividend by 3. Remember, although the first figure of the divisor is 2 because the second figure is 9 we add 1 to the value of the first figure of the divisor and use that in the division. 6 divided by 3 is 2 so 2 is the next figure of our answer.
We repeat steps 2 to 4 but now use the second figure of the answer in the calculations.
Step 5
Calculate the NT product by multiplying the divisor by the second figure we have for the answer.
Multiplying 2 by 2 we get the N value of 04 and multiplying 9 by 2 we get the T value of 1, adding these together we get the NT value of 05.
We subtract the NT value from our partial dividend.
So we put the 1 up in the working figure row below the next figure in the dividend, the 9.
Step 6
We bring down the next figure of the divisor, the 9, down next to the 1 to create our second working figure, 19.
We now calculate the U product by multiplying the units figure of the divisor by the second figure we have for the answer.
We subtract the U product from the working figure to get the third partial dividend.
So 11 is our next partial dividend, and we will write it below the 19 on our partial dividend row.
Step 7
We now divide the third partial dividend, the 11, by 3 to get the third figure of our answer.
Although we have the answer at this point it is not confirmed, the remaining steps besides checking if there is any remainder will also be used to confirm our result.
Remainder Step 1
Calculate the NT product by multiplying the divisor by the third figure we have for the answer.
Multiplying 2 by 3 we get the N value of 06 and multiplying 9 by 3 we get the T value of 2, adding these together we get the NT value of 08.
We subtract the NT value from our partial dividend.
So we put the 3 up in the working figure row below the next figure in the dividend, the 6.
Remainder Step 2
We bring down the next figure of the divisor, the 6, down next to the 3 to create our third working figure, 36.
We now calculate the U product by multiplying the units figure of the divisor by the third figure we have for the answer.
We subtract the U product from the working figure to get the fourth partial dividend.
We have a problem. Our partial dividend, which in this case is also the remainder, is 29, the same value as the divisor. If the remainder is the same or larger than the divisor, it means that the last figure of our answer is too small and should be increased.
In this case, it is easy to see that if the remainder is the same as the divisor, our final result should be 624 instead of 623.
However, it may not always be so clear, the best thing to do is to go back to step 7 and add one to our figure.
Step 7 Try 2
We divided the partial dividend by 3, and we got 3
However, we now know this is too small so we will use 4 instead.
We will redo the remaining steps to confirm our result.
Remainder Step 1 Try 2
Calculate the NT product by multiplying the divisor by the third figure we have for the answer.
Multiplying 2 by 4 we get the N value of 08 and multiplying 9 by 4 we get the T value of 3, adding these together we get the NT value of 11.
We subtract the NT value from our partial dividend.
So we put the 0 up in the working figure row below the next figure in the dividend, the 6.
Remainder Step 2 Try 2
We bring down the next figure of the divisor, the 6, down next to the 0 to create our third working figure, 06.
We now calculate the U product by multiplying the units figure of the divisor by the third figure we have for the answer.
We subtract the U product from the working figure to get the fourth partial dividend.
6-6=0
6-6=0
Now the last partial dividend is zero so we have no remainder, and so we have confirmed that our result is 624.
PRACTICE SOME QUESTIONS AND BE PERFECT.
ALL THE BEST!!!!!!!!!














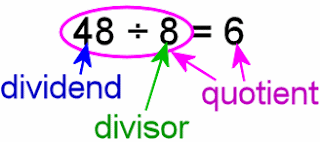





















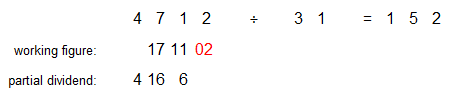






























Comments
Post a Comment